數學視角

函數合成的定義

若 f 和 g 是兩個函數，且 g 的輸出值在 f 的定義域內，則合成函數 f ∘ g
定義為：

g ∘ f(x) = g(f(x))，其中x 是輸入值，如下圖所示。

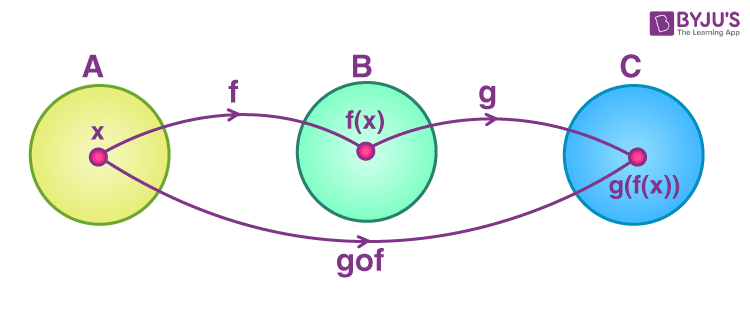
[圖片來源：https://cdn1.byjus.com/wp-content/uploads/2021/05/composite-functions.png]

我們用下面的例子來說明，

假設 g(x) = x² 和 f(x) = x + 3，

則合成函數 g ∘ f 為：
( g ∘ f)(x) = g(f(x)) = g(x + 3) = (x + 3)²

這表示先將 x 加上 3，再將結果平方。

另外，合成函數 f ∘ g 則為：

( f ∘ g)(x) = f(g(x)) = f(x² ) = x² + 3

這表示先將 x 平方，再將結果加上 3。

很明顯的， f ∘ g和 f ∘ g 不是相同的函數

我們再加上一個 h(x)=2x ，並且計算三個函數的合成。

計算 ( f ∘ g) ∘h：

1. 先計算 f ∘ g：

   ( f ∘ g)(x) = f(g(x)) = f(x + 3) = (x + 3)²

2. 再將 h(x) 代入 ( f ∘ g) ：

   (( f ∘ g) ∘h)(x) = ( f ∘ g)(h(x)) = ( f ∘ g)(2x) = (2x + 3)²

   展開後：

   (2x + 3)² = 4x² + 12x + 9

計算 f ∘(g ∘h) ：

1. 先計算 g ∘h ：

   (g ∘h)(x) = g(h(x)) = g(2x) = 2x + 3

2. 再將 g ∘h 代入 f：

   (f ∘(g ∘h))(x) = f((g ∘h)(x)) = f(2x + 3) = (2x + 3)²

   展開後：

   (2x + 3)² = 4x² + 12x + 9

( f ∘ g) ∘h = f ∘(g ∘h) = 4x² + 12x + 9 。

1. 必須確保 g 的輸出值在 f 的定義域內，否則合成函數無法定義。
2. 合成函數不滿足交換率，所以合成的順序很重要， f ∘ g 和 g ∘ f 通常是不同的函數。
3. 函數的合成滿足結合律 ( f ∘ g) ∘h = f ∘(g ∘h)

總結來說，合成函數是將函數的運算過程串聯起來，形成一個新的函數，將來在函數式程式設計是很核心的概念。

反函數的定義和性質：

反函數在數學上也是很重要的觀念，雖然程式設計中較少使用，但是在密碼學中，我們會使用到反函數的觀念，所以也利用這個機會，做一些介紹。

反函數就是將原來的對應域轉變為定義域，而原來的定義域則變為對應域的反對應。為了能夠滿足函數的定義，原來的對應域內的每一個值都被對應到，如此才能夠定義反函數。
若函數 f 是一個一對一函數（即每個輸出值對應唯一的輸入值），則存在一個反函數 f⁻¹ ，滿足：

f⁻¹(f(x)) = x 且 f(f⁻¹(y)) = y

其中，x 是 f 的輸入值， y 是 f 的輸出值。

將函數看成像數字的個體(抽象化)，函數的合成(∘) 可以視為兩個函數相乘，而identity函數x => x可以視為函數的合成運成的1， g ∘ f = 1，可得 g = 1 / f = f⁻¹，這就是合成函數採用「∘」的符號，f的反函數採用f⁻¹的原因。

1. 定義域與值域：

   • f 的定義域是 f⁻¹ 的值域。
   • f 的值域是 f⁻¹ 的定義域。

2. 合成函數：

   • f⁻¹(f(x)) = x 對所有 x 在 f 的定義域內成立。
   • f(f⁻¹(y)) = y 對所有 y 在 f 的值域內成立。

例子 1：線性函數

設 f(x) = 2x + 3 ，求其反函數 f⁻¹(x) 。

步驟：

1. 將 y = f(x) 表示為：

   y = 2x + 3

2. 交換 x 和 y ：

   x = 2y + 3

3. 解出 y ：

   x - 3 = 2y

   y = (x - 3) / 2

4. 因此，反函數為：

   f⁻¹(x) = (x - 3) / 2

驗證：

• f(f⁻¹(x)) = f((x - 3) / 2) = 2( (x - 3) / 2 ) + 3 = x 。
• f⁻¹(f(x)) = f⁻¹(2x + 3) = ((2x + 3) - 3) / 2 = x 。

例子 2：指數函數與對數函數

有時候，原函數的對應域中，並非每個值都被對應到，此時則必須將定義域縮小至值域，如此才能定義反函數，指數函數和對數函數就是很好的例子。因為指數函數的值永遠都大於0，所以對數函數的定義域就不能是整個實數 R ，而是限縮到大於0的實數。
設 f(x) = eˣ ，求其反函數。

步驟：

1. 將 y = f(x) 表示為：

   y = eˣ

2. 交換 x 和 y ：

   x = e^y

3. 解出 y ：

   y = ln(x)

4. 因此，反函數為：

   f⁻¹(x) = ln(x)

驗證：

• f(f⁻¹(x)) = f(ln(x)) = eˡⁿ⁽ˣ⁾ = x 。
• f⁻¹(f(x)) = f⁻¹(eˣ) = ln(eˣ) = x 。

以上兩個公式，很多學生都無法完全了解，大都是用背的，就是不了解反函數的概念。用生活一點的語言來說，如果張三的爸爸是陳六，這兩個公式就相當於問「李四的兒子的爸爸是誰？」和「張三的爸爸的兒子是誰？」這兩個問題。第一個問題「李四的兒子的爸爸是誰？」，由父親對應到兒子和由兒子對應到父親相當於反函數的關係，因此我們並不需要求出李四的兒子是誰，也可以知道「李四」的兒子的爸爸是「李四」，甚至將「李四」改成任何人，這個敘述都永遠是對，也就是「王五」的兒子的爸爸是「王五」，「陳六」的兒子的爸爸是「陳六」…。

總結：

反函數是將函數的輸入和輸出交換的函數，僅當原函數是一對一函數時才存在。通過限制定義域，某些非一對一函數（如二次函數）也可以定義反函數。反函數在數學中有廣泛的應用，例如在解方程、函數圖形的對稱性分析等方面。

程式設計的視角

程式的工作就是將資料經過一個個流程處理，得到的輸出再成為下一個函數的輸入，從資料的角度，而這種資料流的觀念恰恰與函數的合成不謀而合，用資料輸出入的角度看函數的合成就如同下圖

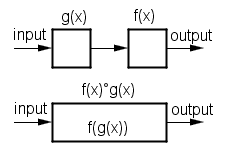
[圖片來源：https://cdn1.byjus.com/wp-content/uploads/2021/05/composite-functions.png]

因此我們程式設計的工作就是設計許多的函數，再將它們合成起來。因此程式設計的工作就變成了「接管」， 將一些資料流動的管線接起來（pipe），或是完成資料的流動（flow）就是函數式程式設計理念的核心。

如果學過unix作業系統的人，對pipe(|)的觀念或名詞應該並不陌生，你可以將一個小程式的輸出結果作為另一個程式的輸入，例如：

ls -l | wc -l // 將ls -l的輸出結果給wc -l當作輸入

fp-ts函式庫既然作為函數式程式設計的框架，提供了pipe和flow兩個函數，讓們進行函數的合成。flow可以直接將多個函數合成起來，也就是所謂的pointfree的形式，pipe則是將函數串接起來之後，再將參數傳入第一個函數。

import { pipe, flow } from 'fp-ts/function'
const add = (x: number) => x + 1;
const multiply = (x: number) => x * 2;
const multiplyAfterAddPointfree = flow(add, multiply);
const multiplyAfterAdd = (x: number) => pipe(x, add, multiply);

學習函數合成的時候，最重要的一點就是保持資料型別的可合成性，也就是前一個函數的輸出型別必須和後一個函數的輸入型別相同，否則會發生錯誤，下面我們就看一些簡單的例子。

const add = (x: number) => x + 1;
const length = (s: string) => s.length;
const getLengthPlusOne = (s: string) => pipe(s, length, add);

我們先用typescript來實作兩個函數的合成：

function compose2<A, B, C>(f: (x: A) => B, g: (x: B) => C): (x: A) => C {
    return (x: A) => g(f(x));
}

由於pipe和flow兩個函數所合成的順序是由前而後(由左而右)，有的人會比較喜歡使用由右而左的順序，接下來我們將實作由右而左(由後而前)n個函數的合成-compose函數。

我們前面提到過兩個函數的合成相當於兩個數字的相乘，如果我們想要讓一個函數裏所有型別為數字的參數相乘，下面是最簡單的作法。

const multiply2 = (x: number, y: number) => x * y;
const multiplyAll = (...args: number[]) => args.reduceRight(multiply2);

依樣畫葫藘，我們可以做出自己的compose如下：

type FN = (...args: any[]) => any;
const composeAll = <Fns extends FN[]>(...fns: Fns) => fns.reduceRight(compose2); // 因為方向要從右到左，所以使用reduceRight

兩個函數的寫法如出一轍，這就是抽象化的威力，數字所成的集合裏有1，任何數乘以1其值不變，而函數所成的集合裏有個identity函數，任何函數和identity合成其結果還是原來的函數；數字的乘法有結合律，而函數的合成也滿足結合律，因此自然可以依樣畫葫蘆。

composeAll的實作如此輕鬆，那麼如何處理composeAll的型別呢？

第一步，先判斷參數中的函數是否可合成。在函數合成的條件中，最重要的是前一個函數的的輸出型別等於後一個函數的出入；如果參數中只有一個函數，則沒有上述問題，必然可以合成，所以我們要設一個輔助型別以判斷一個函數型別陣列是否可合成。

type IsFnsComposable<Fns extends FN[]> = Fns extends [infer Head] // 型別陣列是否只一個函數型別
  ? true // 只有一個函數，回傳型別為true型別
  : Fns extends [
      ...infer RestFns extends FN[],
      infer FnLast2 extends FN, // 倒數第二個函數命名 
      infer FnLast1 extends FN // 倒數第一個函數命名
    ] // 型別陣列是否超過二個或等於二個函數型別
  ? Parameters<FnLast2> extends [ReturnType<FnLast1>] // 檢查倒數第二個函數的輸入型別是否等於倒數第一個的輸出型別
    ? IsFnsComposable<[...RestFns, FnLast2]> // 型別(true或false)由倒數第二個函數型別和陣列其餘函數型別決定
    : false // 輸出false型別
  : false; // 輸出false型別
// 測試
type BooleanToNumberFn = (x: boolean) => number;
type NumberToStringFn = (x: number) => string;
type NumberToBooleanFn = (x: number) => boolean;
type StringToBooleanFn = (x: string) => boolean;
type Composable1 = IsFnsComposable<[NumberToBooleanFn]>; // true
type Composable2 = IsFnsComposable<[StringToBooleanFn, NumberToStringFn, BooleanToNumberFn, NumberToBooleanFn]>; // true
type Composable3 = IsFnsComposable<[NumberToStringFn , StringToBooleanFn, BooleanToNumberFn, NumberToBooleanFn]>; // false

第二步，設計composeAll函數的輸出型別如果函數型別陣列為可合成，則其輸出型別為以第一函數的輸出型別為輸出型別，最後一個函數的輸入型別為輸入型別的函數型別；如果函數型別陣列中只有一個函數型別，則此函數型別即為輸出的函數型別。

type Compose<Fns extends FN[]> = IsFnsComposable<Fns> extends true // 是否可合成
  ? Fns extends [infer Head] // 可合成，是否只有一個函數型別
    ? Head // 只有一個函數型別，此函數型別為輸出型別
    : Fns extends [
        infer Head extends FN,
        ...infer RestFns extends FN[],
        infer Tail extends FN
      ] // 是否超過或包含二個函數型別
    ? (...args: Parameters<Tail>) => ReturnType<Head> // 是，所以最後一個輸入型別為輸入型別，第一個輸出型別為輸出型別
    : never // 無法合成
  : never; // 無法合成

// 測試
type Compose1 = Compose<[NumberToBooleanFn]>; // Number -> Boolean
type Compose2 = Compose<
  [StringToBooleanFn, NumberToStringFn, BooleanToNumberFn, NumberToBooleanFn]
>; // Number -> Boolean
type Compose3 = Compose<
  [NumberToStringFn, StringToBooleanFn, BooleanToNumberFn, NumberToBooleanFn]
>; // Never

最後一步，完成composeAll函數型別由於composeAll的參數的數量不確定，和curry一樣，需要使用typescript的函數多載格式來定義型別和函數的實作。

function composeAll<Fns extends FN[]>(...fns: Fns): Compose<Fns>;
function composeAll<Fns extends FN[]>(...fns: Fns) {
  return fns.reduceRight(compose2);
}
// 測試
const double = (n: number) => 2 * n;
const isPoseitiv = (x: number) => (x > 0 ? true : false);
const showBoolean = (b: boolean) => String(b);

const composedFn = composeAll(showBoolean, isPoseitiv, double);
console.log(composedFn(6)); // true
console.log(composedFn(-6)); // false

今日小結

將所有函數看成一個集合，函數的合成就是函數之間的二元運算，扮演著乘法的角色，這種抽象化的概念在HOF中得以實現，也是函數式程式設計的靈魂。在後面進階的發展，所有概念的設計幾乎是繞著讓函數之間的合成能夠順利。今天的標題「接管」是函數式程式設計的風格，沒有太多其它的語法，所有的重心就是如何將函數們順利接管起來。

composeAll函數的型別處理有些技巧，型別的處理比函數本身設計還困難，希望從中也能學習到typescript型別設計的一些技巧。

今天的分享到此告一段落，明天再見。